பின்ன வகுத்தல்

பின்ன வகுத்தல்

ஒரு பின்னத்தை ஒரு முழு எண்ணால் வகுப்பதற்கு, பின்னத்தின் தொகுதியை அந்த முழுஎண்ணால் வகுக்கலாம் அல்லது பகுதியை அந்த முழுஎண்ணால் பெருக்கலாம்.

எடுத்துக்காட்டு: ${\displaystyle {\tfrac {10}{3}}\div 5={\tfrac {10/5}{3}}={\tfrac {10}{3\cdot 5}}={\tfrac {10}{15}}={\tfrac {2}{3}}}$.

ஒரு முழுஎண்ணை (அல்லது பின்னம்) ஒரு பின்னத்தால் வகுப்பதற்கு அந்த எண்ணை பின்னத்தின் தலைகீழியால் பெருக்கலாம்.

எடுத்துக்காட்டு:

${\displaystyle {\tfrac {1}{2}}\div {\tfrac {3}{4}}={\tfrac {1}{2}}\times {\tfrac {4}{3}}={\tfrac {1\cdot 4}{2\cdot 3}}={\tfrac {2}{3}}}$

பின்ன கழித்தல்,பெருக்கல்

பின்ன கழித்தல்

கூட்டலைப் போன்றதே பின்னங்களின் கழித்தலும். இரு பின்னங்களைக் கழிப்பதற்கு அவற்றின் பகுதிகள் ஒன்றாக இருக்க வேண்டும். கழிக்க வேண்டிய இரு பின்னங்களின் பகுதிகள் ஒரே எண்ணாக இல்லையெனில், அவற்றை ஒரே பகுதி கொண்ட பின்னங்களாக மாற்றிக் கொண்ட பின் கழிக்கலாம்.

எடுத்துக்காட்டு:

${\displaystyle {\tfrac {2}{3}}-{\tfrac {1}{2}}={\tfrac {4}{6}}-{\tfrac {3}{6}}={\tfrac {1}{6}}}$

 பின்ன பெருக்கல்

ஒரு பின்னத்தை மற்றொரு பின்னத்தால் பெருக்குதல்

இரு பின்னங்களைப் பெருக்குவதற்கு அவற்றின் தொகுதியைத் தொகுதியாலும், பகுதியைப் பகுதியாலும் பெருக்க வேண்டும்:

${\displaystyle {\tfrac {2}{3}}\times {\tfrac {3}{4}}={\tfrac {6}{12}}}$

பின்னத்தை முழுஎண்ணால் பெருக்குதல்

எந்தவொரு முழுஎண்ணையும் பகுதி 1 கொண்ட பின்னமாகக் கருதலாம் என்பதால் இரு பின்னங்களைப் பெருக்குவதைப் போன்றதே முழுஎண்ணால் பின்னத்தைப் பெருக்குவதும்.

எடுத்துக்காட்டு:

${\displaystyle 6\times {\tfrac {3}{4}}={\tfrac {6}{1}}\times {\tfrac {3}{4}}={\tfrac {18}{4}}}$

கலப்பு பின்னங்களைப் பெருக்குதல்

கலப்பு பின்னம் (பின்னங்களை) தகா பின்னங்களாக மாற்றிக்கொண்டு இரு பின்னங்களைப் பெருக்குவதைப் போல இவற்றையும் பெருக்க வேண்டும்.

எடுத்துக்காட்டு:

${\displaystyle 3\times 2{\tfrac {3}{4}}=3\times \left({\tfrac {8}{4}}+{\tfrac {3}{4}}\right)=3\times {\tfrac {11}{4}}={\tfrac {33}{4}}=8{\tfrac {1}{4}}}$

பின்னக்கூட்டல்

பின்னக்கூட்டல் . 

இரு பின்னங்களைக் கூட்டுவதற்கு முக்கிய தேவையாக அவற்றின் பகுதிகள் சமமானவையாக இருக்க வேண்டும்.

${\displaystyle {\tfrac {2}{4}}+{\tfrac {3}{4}}={\tfrac {5}{4}}=1{\tfrac {1}{4}}}$.

கூட்ட வேண்டிய பின்னங்களின் பகுதிகள் ஒரே எண்ணாக இல்லையெனில், முதலில் அவற்றை ஒரே பகுதிகளைக் கொண்ட சமான பின்னங்களாக மாற்றிக் கொண்டு, பின் கூட்ட வேண்டும்.

எடுத்துக்காட்டுகள்:

• ${\displaystyle {\tfrac {1}{4}}\ +{\tfrac {1}{3}}={\tfrac {1*3}{4*3}}\ +{\tfrac {1*4}{3*4}}={\tfrac {3}{12}}\ +{\tfrac {4}{12}}={\tfrac {7}{12}}}$.
• ${\displaystyle {\tfrac {3}{5}}={\tfrac {3}{5}}\times {\tfrac {3}{3}}={\tfrac {9}{15}}}$

${\displaystyle {\tfrac {2}{3}}\times {\tfrac {5}{5}}={\tfrac {10}{15}}}$.

${\displaystyle {\tfrac {3}{5}}+{\tfrac {2}{3}}={\tfrac {9}{15}}+{\tfrac {10}{15}}={\tfrac {19}{15}}=1{\tfrac {4}{15}}}$

பின்னங்களை ஒப்பிடல்

பின்னங்களை ஒப்பிடல்

• ஒரே பகுதிகளைக் கொண்ட பின்னங்களை அவற்றின் தொகுதிகளை ஒப்பிடுவதன் மூலம் ஒப்பிடலாம். பகுதிகள் ஒன்றாக இருக்கும்போது பெரிய தொகுதியுடைய பின்னமே சிறிய தொகுதி கொண்ட பின்னத்தை விடப் பெரியதாகும்.

${\displaystyle {\tfrac {3}{4}}>{\tfrac {2}{4}}}$

• இரு பின்னங்கள் ஒரே தொகுதி கொண்டிருந்தால், சிறிய பகுதி கொண்ட பின்னமே பெரிய பகுதி கொண்ட பின்னத்தைவிடப் பெரியதாகும்.

${\displaystyle {\tfrac {4}{3}}>{\tfrac {4}{5}}}$

இரு பின்னங்களை ஒப்பிடுவதற்கு, அவற்றின் பகுதிகளைச் சமமானவைகளாக மாற்றுவது ஒரு வழிமுறையாகும்.

${\displaystyle {\tfrac {a}{b}}}$, ${\displaystyle {\tfrac {c}{d}}}$ இரண்டையும் ஒப்பிடுவதற்கு அவை பின்வருமாறு சமான மாற்றப்படுகின்றன:

${\displaystyle {\tfrac {a}{b}}={\tfrac {ad}{bd}}}$

${\displaystyle {\tfrac {c}{d}}={\tfrac {bc}{bd}}}$

இரண்டின் பகுதிகளும் ஒன்றாக உள்ளன. எனவே தொகுதிகளான ad , bc இரண்டையும் ஒப்பிடுவதன் மூலம் இவ்விரு பின்னங்களில் எது பெரியது, எது சிறியது எனத் தீர்மானிக்கலாம்.

எடுத்துக்காட்டு:

${\displaystyle {\tfrac {2}{3}}}$, ${\displaystyle {\tfrac {1}{2}}}$

சம பகுதிகளைக் கொண்டச் சமான பின்னங்களைக் காண:

${\displaystyle {\tfrac {2}{3}}={\tfrac {4}{6}}}$; ${\displaystyle {\tfrac {1}{2}}={\tfrac {3}{6}}}$

${\displaystyle {\tfrac {4}{6}}>{\tfrac {3}{6}}}$

${\displaystyle {\tfrac {2}{3}}>{\tfrac {1}{2}}}$

ஆறாம் வகுப்பு மாணவர்களுக்கு இன்று நடத்தினேன்.

எண்

எண் (Number) என்பது எண்ணுதல், அளவிடுதல் மற்றும் சிட்டையிடுதலுக்குப் பயன்படும் ஒரு கணிதப் பொருளாகும். கணிதத்துறையில் பலவகையான எண்கள் உள்ளன. எண்களுக்கான இயல் எண்கள் (1, 2, 3, 4, ...) எண்களுக்கான அடிப்படை எடுத்துக்காட்டாகும். எண்களைக் குறிப்பதற்குப் பயன்படுத்தப்படும் குறியீடானதுஎண்ணுரு எனப்படும்.

மனிதன் தோன்றிய காலத்திலேயே அவன் கைவிரல்களை எண்ண எப்பொழுது தானே கற்றுக்கொண்டானோ அன்றே 'எண்' என்ற கருத்து உண்டானதாகக் கொள்ளலாம். எண்களின் கருத்து வளர்ச்சியே கணிதவியலின் தோற்றம் ஆகும்.

கணிதத்தில், பல நூற்றாண்டுகளாக பூச்சியம் எதிர்ம எண்கள், விகிதமுறு எண்கள்({{math|12, −23), மெய்யெண்கள், (√2]], π), சிக்கல் எண்கள்  என எண்களின் தொகுப்பு நீட்சியடைந்தது. எண்கணிதத்தில் கூட்டல், கழித்தல், பெருக்கல், வகுத்தல், அடுக்கேற்றம்ஆகிய கணிதச் செயலிகளின் மூலம் எண்கள் கணிக்கிடப்படுகின்றன. எண் கோட்பாட்டில் எண்களின் பண்புகள் விளக்கப்படுகிறது.

எண் என்ற கருத்துரு தொன்மக் காலம் தொட்டு தமிழர்களிடம் முக்கியத்துவம் பெற்றிருக்கின்றது. "எண்ணென்ப ஏனை எழுத்தென்ப; இவ்விரண்டும் கண்ணென்ப வாழும் உயிர்க்கு" என்ற திருவள்ளுவர் குறளும், "எண் எழுத்து இகழேல்" என்ற ஒளவையார் கூற்றும் பழந்தமிழர் சிந்தனையில் எண்ணுக்கும், எழுத்துக்கும் தொன்றுதொட்டு தந்த முக்கியத்துவத்தை விளக்குகின்றன.

தகு பின்னங்கள்,தகா பின்னங்கள்,கலப்பு பின்னங்கள்

தகு பின்னங்களும் தகா பின்னங்களும்

எளிய பின்னங்களை தகு அல்லது தகா பின்னங்களாக வகைப்படுத்தலாம். பகுதியும் தொகுதியும் நேர்ம எண்களாகக் கொண்ட ஒரு பின்னத்தின் தொகுதியானது, அதன் பகுதியை விடச் சிறியதாயின் அப்பின்னம் தகு பின்னம் எனப்படும். மாறாக, அதன் தொகுதியானது, பகுதியை விடப் பெரியதாயின் அப்பின்னம் தகா பின்னம் எனப்படும். பொதுவாக, ஒரு பின்னத்தின் தனி மதிப்பு 1 ஐ விடச் சிறியதாக இருந்தால் (-1 ஐ விடப் பெரியது, 1 ஐ விட சிறியது) அது ஒரு தகு பின்னமாகும்.ஒரு பின்னத்தின் தனி மதிப்பு 1 க்குச் சமமாகவோ அல்லது பெரியதாக இருந்தால் அது ஒரு தகா பின்னமாகும்.

எடுத்துக்காட்டுகள்:

தகு பின்னங்கள்: 2/3, -3/4, 4/9

தகா பின்னங்கள்: 9/4, -4/3, 3/3.

கலப்பு பின்னங்கள்

கலப்பு பின்னம் அல்லது கலப்பு எண் என்பது, ஒரு பூச்சியமற்ற முழுஎண் மற்றும் தகுபின்னம் இரண்டின் கூடுதலாக அமையும். முழுஎண்ணுக்கும் தகுபின்னத்துக்கும் இடையே "+" குறியீடு எழுதப்படுவதில்லை.

எடுத்துக்காட்டு:

${\displaystyle 2+{\frac {3}{4}}=2{\tfrac {3}{4}}}$.

இயற்கணிதத்தில் இரு கோவைகளின் பெருக்கலை எழுதும்போது அவற்றுக்கிடையே பெருக்கல் குறியானது இல்லாமலே எழுதுவது வழக்கில் உள்ளது. எடுத்துக்காட்டாக, இயற்கணிதத்தில் ${\displaystyle a{\tfrac {b}{c}}}$ என்பது ஒரு கலப்பு பின்னம் அல்ல, அது a, b/c ஆகிய இரு கோவைகளின் பெருக்கலாகும்: ${\displaystyle a{\tfrac {b}{c}}=a\times {\tfrac {b}{c}}}$.

இக்குழப்பத்தைத் தவிர்ப்பதற்கு, பெருக்கல் குறி வெளிப்படையாகக் குறிக்கப்படுகிறது:

${\displaystyle a{\tfrac {b}{c}}=a\times {\tfrac {b}{c}}}$,

${\displaystyle a\cdot {\tfrac {b}{c}}}$,

${\displaystyle a({\tfrac {b}{c}})}$.

கலப்பு பின்னத்தைத் தகா பின்னமாகவும் தகா பின்னத்தைக் கலப்பு பின்னமாகவும் மாற்றலாம்:

கலப்பு பின்னங்கள்

கலப்பு பின்னங்கள்

கலப்பு பின்னம் அல்லது கலப்பு எண் என்பது, ஒரு பூச்சியமற்ற முழுஎண் மற்றும் தகுபின்னம் இரண்டின் கூடுதலாக அமையும். முழுஎண்ணுக்கும் தகுபின்னத்துக்கும் இடையே "+" குறியீடு எழுதப்படுவதில்லை.

எடுத்துக்காட்டு:

.

இயற்கணிதத்தில் இரு கோவைகளின் பெருக்கலை எழுதும்போது அவற்றுக்கிடையே பெருக்கல் குறியானது இல்லாமலே எழுதுவது வழக்கில் உள்ளது. எடுத்துக்காட்டாக, இயற்கணிதத்தில்  என்பது ஒரு கலப்பு பின்னம் அல்ல, அது a, b/c ஆகிய இரு கோவைகளின் பெருக்கலாகும்: .

இக்குழப்பத்தைத் தவிர்ப்பதற்கு, பெருக்கல் குறி வெளிப்படையாகக் குறிக்கப்படுகிறது:

,

,

.

கலப்பு பின்னத்தைத் தகா பின்னமாகவும் தகா பின்னத்தைக் கலப்பு பின்னமாகவும் மாற்றலாம்.

கூம்பு

கூம்பு

கூம்பு என்பது ஒரு வடிவவியல் (இலங்கை வழக்கு: கேத்திர கணிதம்) திண்மம் ஆகும். செங்கோண முக்கோணம்ஒன்றை அதன் சிறிய பக்கங்களுள் ஒன்றை அச்சாகக் கொண்டு சுழற்றும் போது இது உருவாகின்றது. மற்றச் சிறிய பக்கத்தின் சுழற்சியினால் உருவாகும் தட்டு அக்கூம்பின் அடி எனப்படும். இந்த அடியில் அமையாத, அச்சின் மறுமுனை கூம்பின் உச்சி என அழைக்கப்படுகின்றது.

கூம்பின் உச்சியோடு சேர்ந்த மேல்பகுதி, அதன் அடிக்கு இணையான தளம் ஒன்றினால் வெட்டப்படும் போது உருவாகும் கீழ்த் துண்டு, கூம்பினடித்துண்டு எனப்படுகின்றது.

r என்னும் அடித்தட்டு ஆரையையும், h உயரத்தையும் கொண்ட ஒரு கூம்பின் கனவளவு V:

${\displaystyle V=\pi r^{2}h/3}$ என்னும் சூத்திரத்தால் கொடுக்கப்படுகின்றது. இது அதே அளவிகளைக் கொண்ட உருளை ஒன்றின் கனவளவின் மூன்றில் ஒரு பங்கு ஆகும்.

கூம்பொன்றின் மேற்பரப்பின் பரப்பளவு ${\displaystyle A}$:

${\displaystyle A=\pi r(r+s)}$, என்னும் சமன்பாட்டால் தரப்படுகின்றது.

மொத்த மேற்பரப்பு = அடிப்பரப்பு + வளைபரப்பு

                                     

விகிதமுறு எண்கள்

விகிதமுறு எண்கள்

அரை, கால், ஒன்றேமுக்கால் என்பன போன்று முழு எண்களால் ஆன விகிதங்களால் குறிப்பிடப்படுவன ஒரு வகுகோட்டின் மேலும் கீழுமாக முழு எண்களால் குறிப்பிடப்படும் வகுனி எண்கள் அல்லது விகிதமுறு எண்கள் (rational numbers) எனப்படும். இவை அரை கால், வீசம் போன்ற கீழ்வாய் எண்களாக அல்லது குறைஎண்களாக (பின்னங்கள், பிள்வங்கள்) இருக்கலாம், அல்லது 7/3, 21/6 என்பன போன்று ஒன்றின் மிகையான எண் அளவைக்குறிக்கும் எண்களாகவும் இருக்கலாம். இவ் வகுனி எண்கள் கணம் ${\displaystyle \mathbf {Q} }$ என்னும் எழுத்தால் குறிக்கப்படுகின்றது.

இந்த விகிதமுறு கணம் ${\displaystyle \mathbf {Q} }$ முழு எண்களின் கணமான ${\displaystyle \mathbf {Z} }$ ஐ உள்ளடக்கியது. அதாவது ${\displaystyle \mathbf {Z} \subset \mathbf {Q} }$

இயல் எண்கள்,முழு எண்கள்

இயல் எண்கள்

நடைமுறையில் மிகவும் பழக்கமான எண்கள், எண்ணுவதற்குப் பயன்படும் எண்கள் இயற்கை எண்களாகும். இவைகளைஇயல் எண்கள் அல்லது இயலெண்கள் என்றும் குறிப்பிடலாம். இவை 1, 2, ... என்பன.

இவ்வெண் தொகுதி (கணம்) ${\displaystyle \mathbf {N} }$ என்னும் சிறப்பெழுத்தால் கணிதத்தில் குறிக்கப்படுகின்றது.

முழு எண்கள்

இயல் எண்களுடன் பூச்சியம் மற்றும் எதிர்ம எண்களையும் (-1, -2, -3, ...) சேர்த்து, முழு எண்கள் கணம் அமைகிறது. இக்கணத்தின் குறியீடு ${\displaystyle \mathbf {Z} }$ ஆகும்.

முழு எண்கள் மூன்று வகைப்படும்:

• மிகை எண்கள் அல்லது நேர்ம எண்கள்: 1, 2, 3, ...

• பூச்சியம் அல்லது சூனியம்: 0

• குறை எண்கள் அல்லது எதிர்ம எண்கள்: -1, -2, -3, ...

இம்முழு எண்களின் கணம் ${\displaystyle \mathbf {Z} }$ இயல் எண்களின் கணமான ${\displaystyle \mathbf {N} }$ ஐ உள்ளடக்கியது. அதாவது $$

கார்ட்டீசியன் ஆய முறைமை

கார்ட்டீசியன் ஆய முறைமை

 கார்ட்டீசியன் ஆய முறைமை (Cartesian coordinate system) என்பது, இட வெளியில் உள்ள ஒவ்வொரு புள்ளியையும் துல்லியமாய்க் குழப்பம் ஏதும் இன்றிக் குறிக்கப் பயன்படும் ஒரு முறை. எடுத்துக்காட்டாக ஒரு தளத்திலுள்ள புள்ளிகள் ஒவ்வொன்றையும் இரண்டு எண்கள்மூலமாக இம்முறைப்படி வேறுபடுத்திக் குறிக்கலாம். இந்த இரண்டு எண்களும் குறிப்பிட்ட தொடக்கப் புள்ளியில் இருந்து அளந்தறியப்படும். இவை x- ஆள்கூறு, y- ஆள்கூறு என அழைக்கப்படுகின்றன. ஆள்கூறுகளைத் தீர்மானிப்பதற்காக ஒன்றுக்கொன்று செங்குத்தான இரண்டு கோடுகள் வரையப்படுகின்றன இவைதான் ஒப்பீட்டுச் சட்டக் கோடுகள். இவை x- அச்சு, y- அச்சு எனப்படுகின்றன. x- அச்சைக் கிடை நிலையிலும், y- அச்சைநிலைக்குத்தாகவும் வரைவது மரபாகும். இக்கோடுகள் ஒன்றையொன்று வெட்டும் புள்ளி தொடக்கப்புள்ளிஎனப்படும். 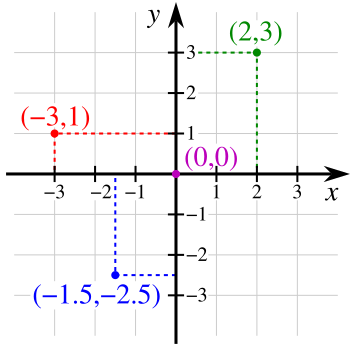இப்புள்ளியிலிருந்து தொடங்கி அச்சுக்கள் வழியே அருகிலுள்ள படத்தில் காட்டியபடி, அளவுகள் குறிக்கப்படுகின்றன. இவ்விரு அச்சுக்களும் உள்ள தளத்திலுள்ள ஏதாவது ஒரு புள்ளி, இவ்விரு அச்சுக்களிலும் இருந்து எவ்வளவு தூரத்தில் இருக்கிறது எனக் குறிப்பதன்மூலம் அப்புள்ளியை ஏனைய புள்ளிகளிலிருந்து வேறுபடுத்தி அறியலாம். அதாவது அவ்விரு எண்களும், குறிப்பிட்ட புள்ளிக்குரிய தனித்துவமான இயல்பு ஆகும். y- அச்சிலிருந்து ஒரு புள்ளியின் தூரம் அப்புள்ளியின் x- ஆள்கூறு ஆகும். x- அச்சிலிருந்து அதன் தூரம், y- ஆள்கூறு ஆகும். ஒரு புள்ளியின் x- ஆள்கூறு 2 அலகு ஆகவும், y- ஆள்கூறு 3 அலகுகளாகவும் இருப்பின் அப்புள்ளியை (2,3) எனக் குறிப்பது மரபு.

ஒரு தளத்தில் மட்டுமன்றிக் காட்டீசியன் ஆள்கூற்று முறைமையை முப்பரிமாண வெளியிலும் பயன்படுத்த முடியும். இதன்மூலம் ஒரு இட "வெளி"யில் உள்ள புள்ளியொன்றை வேறுபடுத்திக் குறிக்க முடியும். இதற்கு ஒன்றுக்கொன்று செங்குத்தான மூன்று திசையில் உள்ள கோடுகள் பயன்படுகின்றன. அதாவது இங்கே 3 அச்சுகள் இருக்கும். மூன்றாவது அச்சு z-அச்சு ஆகும். இதனால் இட வெளியில் உள்ள ஒரு புள்ளியைக் குறிப்பிட மூன்று அச்சுகளிலிருந்தும் அளக்கப்படும் தொலைவுகளைக் (x, y, z) கொடுப்பதன்மூலம் குறிக்கப்படுகின்றது.

காட்டீசியன் ஆள்கூற்று முறைமையைப் பயன்படுத்தி, வடிவகணித வடிவங்களைச் சமன்பாடுகள் மூலம் குறிக்கமுடியும். அதாவது, குறித்த வடிவத்திலுள்ள ஒவ்வொரு புள்ளியின் x, y ஆள்கூறுகளுக்கு இடையேயான கணிதத் தொடர்பை ஒரு சமன்பாடடால் முற்றிலுமாய் விளக்க முடியும். எடுத்துக்காட்டாக, 2 அலகு ஆரையைக் கொண்ட வட்டம் ஒன்றை x² + y² = 2² எனக் குறிப்பிடலாம்.

   

உருளை

உருளை:

உருளை(cylinder) என்பது, அடிப்படை வளைகோட்டு வடிவங்களில் ஒன்றாகும். தரப்பட்ட ஒரு கோட்டுத் துண்டிலிருந்து மாறாத தூரத்தில் அமையும் புள்ளிகளால் உருவாகும் பரப்பு உருளையாகும். தரப்பட்ட அந்தக் கோட்டுத் துண்டு உருளையின் அச்சு எனப்படும். இப்பரப்பாலும் மேலும் அச்சுக்கு செங்குத்தான இரு தளங்களாலும் அடைபடும் திடப்பொருளும் உருளை எனப்படும். உருளையின் புறப்பரப்பும் கன அளவும் பண்டைக்காலத்திலேயே அறியப்பட்டிருந்திருக்கின்றன. வகையீட்டு வடிவவியலில், உருளையானது இன்னும் பரந்த அளவில், ஒரு துணையலகில் அமைந்த இணைகோடுகளின் குடும்பத்தால் நீட்டிக்கப்பட்ட, கோடிட்ட பரப்பாக வரையறுக்கப்படுகிறது. ஒரு உருளையின் வெட்டுப்பகுதி,

• நீள்வட்டமாக இருந்தால் அது நீள்வட்ட உருளை;
• பரவளையமாக இருந்தால் அது பரவளைய உருளை;
• அதிபரவளையமாக இருந்தால் அது அதிபரவளைய உருளை ஆகும்.                                                                  
  
  உருளையின் ஆரம் r மற்றும் நீளம்(உயரம்) h எனில், அதன் கன அளவு:
  V = πr²h