கோணம்:
ஒரே புள்ளியில் இருந்து கிளம்பும் இரண்டு கதிர்கள் உருவாக்கும் வடிவம் கோணம் (Angle) எனப்படுகிறது[1]. வெட்டிக்கொள்ளும் இரண்டு கோடுகளின் சாய்வுகளின் வித்தியாசம் காண கோணம் உதவுகிறது. கோணங்களை அளக்கும் அலகுகளுள் பாகை ஒரு வகையாகும். இதன் குறியீடு °.

கோணத்தின் வகைகள் :
செங்கோணம், குறுங்கோணம், விரிகோணம், நேர்கோணம், சாய்வுக் கோணம், பின்வளைகோணம்
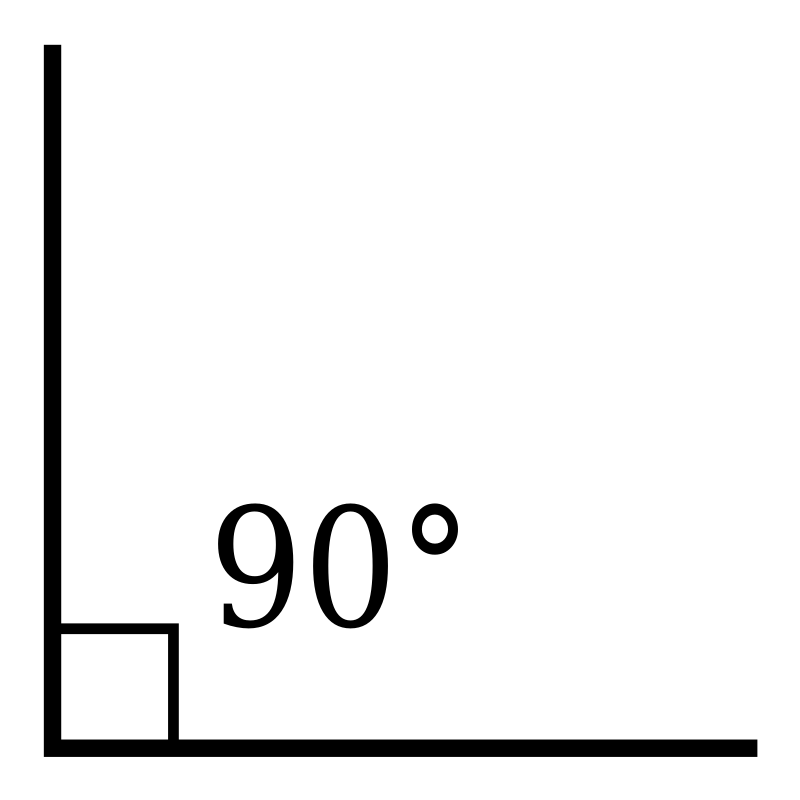
90 பாகை அளவுள்ள கோணம், செங்கோணம் எனக் குறிப்பிடப்படுகின்றது. இரு நேர்கோடுகள் ஒன்றோடு ஒன்று முட்டும்போது அவற்றுக்கு இடைப்பட்ட கோணம் சரியாக 90 பாகையாக இருந்தால் அது செங்கோணம் எனப்படும்.
ஒரே புள்ளியில் இருந்து கிளம்பும் இரண்டு கதிர்கள் உருவாக்கும் வடிவம் கோணம் (Angle) எனப்படுகிறது[1]. வெட்டிக்கொள்ளும் இரண்டு கோடுகளின் சாய்வுகளின் வித்தியாசம் காண கோணம் உதவுகிறது. கோணங்களை அளக்கும் அலகுகளுள் பாகை ஒரு வகையாகும். இதன் குறியீடு °.

கோணத்தின் வகைகள் :
செங்கோணம், குறுங்கோணம், விரிகோணம், நேர்கோணம், சாய்வுக் கோணம், பின்வளைகோணம்
பூஜ்ஜிய கோணம்
ஒரே புள்ளியில் ஆரம்பிக்கும் இரு கதிர்களுக்கு இடைப்பட்ட தூரம் 0 பாகை எனில் அக்கோணம் பூஜ்ஜிய கோணம் எனப்படும்.
செங்கோணம்:90 பாகை அளவுள்ள கோணம், செங்கோணம் எனக் குறிப்பிடப்படுகின்றது. இரு நேர்கோடுகள் ஒன்றோடு ஒன்று முட்டும்போது அவற்றுக்கு இடைப்பட்ட கோணம் சரியாக 90 பாகையாக இருந்தால் அது செங்கோணம் எனப்படும்.